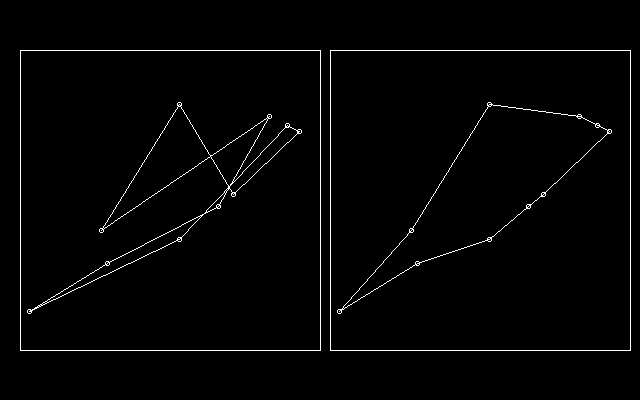
/* anneal.c */
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
/*#define GRAPHICS /* graphics routine on */
/*#define MONITOR /* monitoring flag */
#ifdef GRAPHICS
#include <graphics.h>
#endif
#define TFACTR 0.9 /* アニーリング・スケジュール */
/* t に毎回この値を掛ける。 */
#define ALEN(a,b,c,d) sqrt(((b)-(a))*((b)-(a)) + ((d)-(c))*((d)-(c)))
#define MBIG 1000000000
#define MSEED 161803398
#define MZ 0
#define FAC (1.0 / MBIG)
#define IB1 1
#define IB2 2
#define IB5 16
#define IB18 131072
#ifdef GRAPHICS
void initgraphics(void);
void drawgrid();
void plot(int xo, int yo, double x[], double y[], int iorder[], int ncity);
#endif
void anneal(double x[], double y[], int iorder[], int ncity);
double energy(double x[], double y[], int iorder[], int ncity);
double revcst(double x[], double y[], int iorder[], int ncity, int n[]);
void reverse(int iorder[], int ncity, int n[]);
double trncst(double x[], double y[], int iorder[], int ncity, int n[]);
void trnspt(int iorder[], int ncity, int n[]);
int metrop(double de, double t);
double ran3(long *idum);
int irbit1(unsigned long *iseed);
double *vector(long n);
void free_vector(double *v);
int *ivector(long n);
void free_ivector(int *v);
/*
このアルゴリズムは、ncity 個の町を巡回する最短閉路を求める。町の座標は、
x[1..ncity],y[1..ncity] で与える。配列 iorder[1..ncity] は町を巡る順序を表し、
入力時には 1 から ncity までの整数のどんな順序を入れておいても良い。
出力時には見つかった最良の経路に置き換えられる。
*/
void anneal(double x[], double y[], int iorder[], int ncity)
{
int ans, nover, nlimit, i1, i2;
int i, j, k, nsucc, nn, idec;
static int n[7];
long idum;
unsigned long iseed;
double path, de, t;
nover = 100 * ncity; /* 各温度で試みる経路の最大数 */
nlimit = 10 * ncity; /* 各温度で実際に経路を更新する最大回数 */
path = energy(x, y, iorder, ncity); /* 初期経路長の計算 */
t = 0.5;
idum = -1;
iseed = 111;
for(j = 1; j <= 100; j++) /* 最大 100 段階の温度を試す */
{
nsucc = 0;
for(k = 1; k <= nover; k++)
{
do
{
n[1] = 1 + (int)(ncity * ran3(&idum)); /* 切断部の頭と */
n[2] = 1 + (int)((ncity - 1) * ran3(&idum)); /* 尾を結ぶ */
if(n[2] >= n[1]) ++n[2];
nn = 1 + ((n[1] - n[2] + ncity - 1) % ncity); /* 切断部以外の町の数 */
}while(nn < 3);
idec = irbit1(&iseed);
/*
切断部を元の場所に逆向きに挿入するか、別の場所に移植するかを決める
*/
if(idec == 0) /* 別の場所に移植する */
{
n[3] = n[2] + (int)(abs(nn - 2) * ran3(&idum)) + 1;
n[3] = 1 + ((n[3] - 1) % ncity);
/* その経路以外のところに挿入する */
de = trncst(x, y, iorder, ncity, n); /* コストを計算する */
ans = metrop(de, t); /* 託宣に耳を傾ける */
if(ans)
{
++nsucc;
path += de;
trnspt(iorder, ncity, n); /* 移植を実行する */
}
}
else /* 逆向きにすげ付ける */
{
de = revcst(x, y, iorder, ncity, n); /* コストを計算する */
ans = metrop(de, t); /* 託宣に耳を傾ける */
if(ans)
{
++nsucc;
path += de;
reverse(iorder, ncity, n); /* 反転を実行する */
}
}
if(nsucc >= nlimit) break; /* 実際に経路を更新した回数が十分 */
} /* 多ければループを脱出する */
#ifdef MONITOR
printf("\n %s %10.6f %s %12.6f \n", "T =", t, " Path Length =", path);
printf("Successful Moves : %6d\n", nsucc);
#endif
t *= TFACTR; /* アニーリングスケジュール */
if(nsucc == 0) return; /* 更新が起こらなければ完成 */
}
}
/* 最小化すべき目的関数 */
double energy(double x[], double y[], int iorder[], int ncity)
{
int i, i1, i2;
double e;
e = 0.0;
for(i = 1; i < ncity; i++)
{
i1 = iorder[i];
i2 = iorder[i + 1];
e += ALEN(x[i1], x[i2], y[i1], y[i2]);
}
i1 = iorder[ncity];
i2 = iorder[1];
return e + ALEN(x[i1], x[i2], y[i1], y[i2]);
}
/*
与えられた経路の反転に要するコストを返す。ncity は町の数、x[1..ncity],
y[1..ncity] は各町の座標。iorder[1..ncity] は現在の道順。配列 n の最初の2個の
値 n[1],n[2] が反転すべき経路部分の最初と最後の町。反転のコスト de を返す。
このルーチンは実際の反転をするわけではない。
*/
double revcst(double x[], double y[], int iorder[], int ncity, int n[])
{
double xx[5], yy[5], de;
int j, ii;
n[3] = 1 + ((n[1] + ncity - 2) % ncity); /* n[1] の直前の町 */
n[4] = 1 + (n[2] % ncity); /* n[2] の直後の町 */
for(j = 1; j <= 4; j++) /* 4つの町の座標を求める */
{
ii = iorder[n[j]];
xx[j] = x[ii];
yy[j] = y[ii];
}
de = -ALEN(xx[1], xx[3], yy[1], yy[3]); /* 両端で切断して逆順に */
de -= ALEN(xx[2], xx[4], yy[2], yy[4]); /* 挿入するコストの計算 */
de += ALEN(xx[1], xx[4], yy[1], yy[4]);
de += ALEN(xx[2], xx[3], yy[2], yy[3]);
return de;
}
/*
経路の一部を反転する。iorder[1..ncity] に現在の巡回順序を入れ替えて呼び出す。
ベクトル n の最初の4要素は、反転部分の最初と最後の町 n[1],n[2]、反転部分の
直前と直後の町 n[3],n[4] である。n[3],n[4] は関数 revcst で求める。出力時には
iorder[1..ncity] は n[1] から n[2] までの部分を反転した道順になる。
*/
void reverse(int iorder[], int ncity, int n[])
{
int nn, j, k, l, itmp;
/* これだけの数の町を交換すれば反転したことになる */
nn = (1 + ((n[2] - n[1] + ncity) % ncity)) / 2;
for(j = 1; j <= nn; j++)
{
k = 1 + ((n[1] + j - 2) % ncity); /* 反転すべき部分の両端から */
l = 1 + ((n[2] - j + ncity) % ncity); /* 中心に向かって交換していく */
itmp = iorder[k];
iorder[k] = iorder[l];
iorder[l] = itmp;
}
}
/*
与えられた経路を別の場所に移植するのに要するコストを返す。ncity は町の数、
x[1..ncity],y[1..ncity] は各町の座標。iorder[1..ncity] は現在の道順。配列 n
の最初の2個の値 n[1],n[2] が移植すべき経路部分の最初と最後の町で、これをその
部分以外にある町 n[3] の直後に挿入する。この変更に要するコスト de を返す。
このルーチンは実際の移植をするわけではない。
*/
double trncst(double x[], double y[], int iorder[], int ncity, int n[])
{
double xx[7], yy[7], de;
int j, ii;
n[4] = 1 + (n[3] % ncity);
n[5] = 1 + ((n[1] + ncity - 2) % ncity);
n[6] = 1 + (n[2] % ncity);
for(j = 1; j <= 6; j++)
{
ii = iorder[n[j]];
xx[j] = x[ii];
yy[j] = y[ii];
}
de = -ALEN(xx[2], xx[6], yy[2], yy[6]);
de -= ALEN(xx[1], xx[5], yy[1], yy[5]);
de -= ALEN(xx[3], xx[4], yy[3], yy[4]);
de += ALEN(xx[1], xx[3], yy[1], yy[3]);
de += ALEN(xx[2], xx[4], yy[2], yy[4]);
de += ALEN(xx[5], xx[6], yy[5], yy[6]);
return de;
}
/*
metrop の許可が出ればこのルーチンで実際の経路移植を行う。iorder[1..ncity] が
現在の道順。n[1],n[2] は移植すべき経路部分の最初と最後の町で、この部分を隣り
合う2町 n[3],n[4] の間に挿入する。n[5],n[6] は移植部分の直前、直後の町。
n[4],n[5],n[6] は関数 trncst で求める。iorder には更新された道順が入る。
*/
void trnspt(int iorder[], int ncity, int n[])
{
int m1, m2, m3, nn, j, jj, *jorder;
jorder = ivector(ncity);
m1 = 1 + ((n[2] - n[1] + ncity) % ncity); /* n[1],n[2] 間の町の数 */
m2 = 1 + ((n[5] - n[4] + ncity) % ncity); /* n[4],n[5] 間の町の数 */
m3 = 1 + ((n[3] - n[6] + ncity) % ncity); /* n[6],n[3] 間の町の数 */
nn = 1;
for(j = 1; j <= m1; j++)
{
jj = 1 + ((j + n[1] - 2) % ncity); /* 該当部分をコピーする */
jorder[nn++] = iorder[jj];
}
if(m2 > 0)
{
for(j = 1; j <= m2; j++) /* 次に n[4],n[5] 間をコピー */
{
jj = 1 + ((j + n[4] - 2) % ncity);
jorder[nn++] = iorder[jj];
}
}
if(m3 > 0)
{
for(j = 1; j <= m3; j++) /* 最後に n[6],n[3] 間をコピー */
{
jj = 1 + ((j + n[6] - 2) % ncity);
jorder[nn++] = iorder[jj];
}
}
for(j = 1; j <= ncity; j++) /* jorder を iorder に戻す */
iorder[j] = jorder[j];
free_ivector(jorder);
}
/*
Metropolis のアルゴリズム。目的関数 e が de だけ変化する様な配置替えを許すなら
metrop は1(真)を、許さないなら0(偽)を返す。もし de < 0 なら必ず真を返す
が、そうでなければ確率 exp(-de/t) で真を返す。(t はアニーリングスケジュールで
定められる温度)
*/
int metrop(double de, double t)
{
static long gljdum = 1;
return de < 0.0 || ran3(&gljdum) < exp(- de / t);
}
/*
Knuth の減算法に基づき、0.0 と 1.0 の間の一様乱数を返す。
乱数列を初期化、再初期化するには idum を任意の負の値にする。
*/
double ran3(long *idum)
{
static int inext, inextp;
static long ma[56];
static int iff = 0;
long mj, mk;
int i, ii, k;
if(*idum < 0 || iff == 0)
{
iff = 1; /* 初期化 */
mj = MSEED - (*idum < 0 ? -*idum: *idum);
mj %= MBIG;
ma[55] = mj;
mk = 1;
for(i = 1; i <= 54; i++)
{
ii = (21 * i) % 55;
ma[ii] = mk;
mk = mj - mk;
if(mk < MZ) mk += MBIG;
mj = ma[ii];
}
for(k = 1; k <= 4; k++) /* warm up */
{
for(i = 1; i <= 55; i++)
{
ma[i] -= ma[1 + (i + 30) % 55];
if(ma[i] < MZ) ma[i] += MBIG;
}
}
inext = 0; /* 最初に生成する数の添字を準備。 */
inextp = 31;
*idum = 1;
}
/* 初期化以外ではこの上の行から始める。*/
if(++inext == 56) inext = 1;
if(++inextp == 56) inextp = 1;
mj = ma[inext] - ma[inextp];
if(mj < MZ) mj += MBIG;
ma[inext] = mj;
return mj * FAC;
}
/*
ランダムなビットを整数として返す。iseed の下位18ビットを使う。
iseed は次回の呼び出しのために書き換える。
*/
int irbit1(unsigned long *iseed)
{
unsigned long newbit;
newbit = (*iseed & IB18) >> 17
^ (*iseed & IB5) >> 4
^ (*iseed & IB2) >> 1
^ (*iseed & IB1);
*iseed = (*iseed << 1) | newbit;
return (int)newbit;
}
/* allocate a double vector with subscript range v[nl..nh] */
double *vector(long n)
{
double *v;
v = (double *)malloc((size_t)((n + 1) * sizeof(double)));
if(v == NULL) fprintf(stderr, "Error : allocation failure in ivector().\n");
return v;
}
/* free a double vector allocated with vector() */
void free_vector(double *v)
{
free((char *)v);
}
/* allocate a int vector with subscript range v[nl..nh] */
int *ivector(long n)
{
int *v;
v = (int *)malloc((size_t)((n + 1) * sizeof(int)));
if(v == NULL) fprintf(stderr, "Error : allocation failure in ivector().\n");
return v;
}
/* free a int vector allocated with ivector() */
void free_ivector(int *v)
{
free((char *)v);
}
#ifdef GRAPHICS
void initgraphics(void)
{
int gdriver, gmode, ecode;
gdriver = PC98;
gmode = PC98C16;
initgraph(&gdriver, &gmode, "");
ecode = graphresult();
if(ecode != grOk)
{
fprintf(stderr , "Error : Graphics cannot initialize\n");
fprintf(stderr , " error message [ %s ]\n", grapherrormsg(ecode));
exit(1);
}
}
void drawgrid(int xo, int yo)
{
setcolor(WHITE);
setlinestyle(SOLID_LINE, 0, NORM_WIDTH);
line(xo, yo, xo, yo + 300);
line(xo, yo + 300, xo + 300, yo + 300);
line(xo, yo, xo + 300, yo);
line(xo + 300, yo, xo + 300, yo + 300);
}
void plot(int xo, int yo, double x[], double y[], int iorder[], int ncity)
{
int i, xi1, xi2, yi1, yi2;
xi1 = xo + 3 * (int)x[iorder[1]];
yi1 = yo + 3 * (int)y[iorder[1]];
for(i = 2; i <= ncity; i++)
{
xi2 = xo + 3 * (int)x[iorder[i]];
yi2 = yo + 3 * (int)y[iorder[i]];
circle(xi1, yi1, 2);
line(xi1, yi1, xi2, yi2);
xi1 = xi2;
yi1 = yi2;
}
xi2 = xo + 3 * (int)x[iorder[1]];
yi2 = yo + 3 * (int)y[iorder[1]];
circle(xi1, yi1, 2);
line(xi1, yi1, xi2, yi2);
}
#endif
int main(int argc, char *argv[])
{
double *x, *y;
int *iorder;
int i, ncity;
long iseed = -1;
ncity = 10;
if(argc > 1)
{
ncity = atoi(argv[1]);
if(ncity < 3) ncity = 10;
}
if(argc > 2)
{
i = atoi(argv[2]);
while(i-- > 0) ran3(&iseed);
}
#ifdef GRAPHICS
initgraphics();
#endif
x = vector(ncity);
y = vector(ncity);
iorder = ivector(ncity);
for(i = 1; i <= ncity; i++)
{
x[i] = 100. * ran3(&iseed);
y[i] = 100. * ran3(&iseed);
iorder[i] = i;
}
#ifdef GRAPHICS
drawgrid(20, 50);
printf(" [input] ( energy = %10.3f )", energy(x, y, iorder, ncity));
plot(20, 50, x, y, iorder, ncity);
#else
printf("[ input ]\n");
printf(" ncity = %d\n", ncity);
printf("x : ");
for(i = 1; i <= ncity; i++) printf("%7.3f", x[i]);
printf("\ny : ");
for(i = 1; i <= ncity; i++) printf("%7.3f", y[i]);
printf("\nenergy = %8.3f\n", energy(x, y, iorder, ncity));
#endif
anneal(x, y, iorder, ncity);
#ifdef GRAPHICS
drawgrid(330, 50);
printf(" [output] (energy = %10.3f )", energy(x, y, iorder, ncity));
plot(330, 50, x, y, iorder, ncity);
#else
printf("[ output ]\n");
printf(" ncity = %d\n", ncity);
printf("No.: ");
for(i = 1; i <= ncity; i++) printf("%7d", iorder[i]);
printf("\n x : ");
for(i = 1; i <= ncity; i++) printf("%7.3f", x[iorder[i]]);
printf("\n y : ");
for(i = 1; i <= ncity; i++) printf("%7.3f", y[iorder[i]]);
printf("\nenergy = %8.3f\n", energy(x, y, iorder, ncity));
#endif
return 1;
}
|